OEF vektorski podprostori
--- Uvod ---
Ta modul trenutno vsebuje 8 vaj o podprostorih
v vektorskih prostorih.
Razsežnost preseka
Naj bo U vektorski prostor razsežnosti , in naj bosta
,
njegova podprostora razsežnosti in . Potem je razsežnost preseka
enaka najmanj
in največ
.
Homogeni lin. sistem in razsežnost
Naj bo V podprostor vektorskega prostora R, ki ga določa sistem homogenih linearnih enačb, katerega matrika sistema ima rang . Določite razsežnost prostora V.
Razsežnost vsote
Naj bo U vektorski prostor razsežnosti in naj bosta
,
njegova podprostora razsežnosti in . Potem je razsežnost vsote
enaka najmanj
in največ
.
Podbaza
Naj bo U vektorski prostor razsežnosti in množica B njegova baza. Denimo, da je
njena podmnožica moči , ki določa podprostor V prostora U. Potem je razsežnost dim(U) enaka
.
Podbaza II
Naj bo U vektorski prostor razsežnosti in naj bo B njegova baza. Denimo, da sta
in
dve podmnožici množice B z močjo oziroma , njun presek
pa ima moč . Naj bosta
in
podprostora v U z ogrodjema
oziroma
. Potem je razsežnost preseka
enaka
.
Razsežnost podprostora
Naj bo V vektorski podprostor prostora 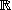 , . Potem je razsežnost dim(V) enaka
.
, . Potem je razsežnost dim(V) enaka
.
Razsežnost podprostora matrik
Naj bo V vektorski podprostor prostora 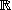 ×, ki vsebuje vse realne × matrike A, za katere velja =0 za neko izbrano neničelno matriko B velikosti ×. Potem je njegova razsežnost dim(V) enaka najmanj
in največ
.
×, ki vsebuje vse realne × matrike A, za katere velja =0 za neko izbrano neničelno matriko B velikosti ×. Potem je njegova razsežnost dim(V) enaka najmanj
in največ
.
Razširitev podprostora
Naj bo V vektorski prostor razsežnosti dim(V)= in U njegov podprostor razsežnosti dim(U)= z ogrodjem S. Naj bo v 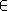 V vektor, ki linearna kombinacija vektorjev iz S, in naj bo U' vektorski podprostor v F z ogrodjem
{v}. Kolikšna je razsežnost prostora U'?
The most recent version
V vektor, ki linearna kombinacija vektorjev iz S, in naj bo U' vektorski podprostor v F z ogrodjem
{v}. Kolikšna je razsežnost prostora U'?
The most recent version
- Description: zbirka vaj o vektorskih podprostorih. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, algebra, linearna algebra, vektorski prostor, podprostor, baza, razsežnost, linearni sistem
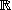 , . Potem je razsežnost dim(V) enaka
.
, . Potem je razsežnost dim(V) enaka
.
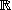 ×, ki vsebuje vse realne × matrike A, za katere velja =0 za neko izbrano neničelno matriko B velikosti ×. Potem je njegova razsežnost dim(V) enaka najmanj
in največ
.
×, ki vsebuje vse realne × matrike A, za katere velja =0 za neko izbrano neničelno matriko B velikosti ×. Potem je njegova razsežnost dim(V) enaka najmanj
in največ
.
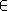 V vektor, ki linearna kombinacija vektorjev iz S, in naj bo U' vektorski podprostor v F z ogrodjem
{v}. Kolikšna je razsežnost prostora U'?
V vektor, ki linearna kombinacija vektorjev iz S, in naj bo U' vektorski podprostor v F z ogrodjem
{v}. Kolikšna je razsežnost prostora U'?